Quadrato 10x10

Ai tempi delle scuole superiori mi ricordo c’era un gioco abbastanza diffuso nella mia classe. Non so esattamente il suo vero nome e forse non lo ha nemmeno e quindi lo chiamerò genericamente Quadrato 10x10. Se qualcuno conosce il suo nome e la sua formulazione originale, me la comunichi. Mi farebbe molto piacere saperlo. Vediamo di descrivere le semplici regole del gioco. Il tabellone di gioco è una matrice (o tabella) 10 x 10, quindi 10 righe e 10 colonne (vedi Figura 1).

Figura 1 - Il tabellone di gioco

Per “vincere” si devono riempire tutte le caselle (o celle) con i numeri dal 1 al 100, senza ripetizioni, seguendo queste tre regole:

1. I numeri devono essere inseriti in ordine crescente partendo dall’‘1 (quindi 1, 2, 3, …, 100 - No 1, 3 , 10, …).
2. Sia n il numero corrente. Il numero n+1 se inserito in verticale o in orizzontale rispetto al numero n va distanziato di 2 caselle (Vedi Figura 2).
3. Il numero n+1 se inserito in obliquo rispetto al numero n va distanziato di 1 casella (Vedi Figura 2).

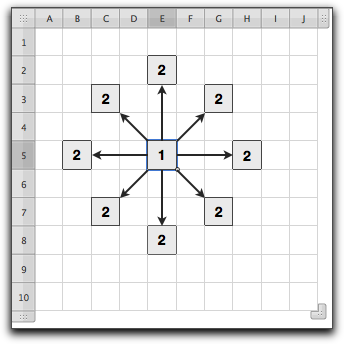
Figura 2 - Movimenti

Per iniziare si può scegliere una cella qualsiasi. Mi ricordo che i miei compagni per anni hanno cercato invano una soluzione, riempiendo pagine e pagine. Qualcuno si era avvicinato al numero 100, ma nessuno mai aveva trovato una soluzione. Come in ogni buona storia si vociferava che un amico di un amico avesse trovato la soluzione, ma nessuno mai l’aveva vista. Ad un certo punto incuriosito mi sono cimentato anch’io nel gioco e dopo averlo provato senza cognizione di causa per qualche volta senza ovviamente successo, ho deciso di affrontarlo in maniera più articolata.

Il primo approccio è stato quello di creare un algoritmo che in gergo informatico viene chiamato a “forza bruta“ (anche noto come ricerca esaustiva della soluzione). Ho scritto un programmino in C che “spazzolava” tutte le possibili combinazioni possibili fino a trovarne una che completasse tutta la matrice. A quei tempi ero ancora uno studente della scuola superiore, quindi non avevo background teorico per capire che un simile metodo difficilmente poteva avere successo, visto che il numero delle possibili combinazioni era un numero considerevole (con 100 elementi il numero totale delle permutazione è 100!).

Dopo un giorno di elaborazione il mio PC, a quel tempo un CompaQ con processore Intel Pentium 100 MHz, non aveva trovato assolutamente nulla. E il mio sesto senso mi diceva che la soluzione era molto lontana. Purtroppo non ho più quel programma in C, ma se mai avrò voglio cercherò di riscriverlo. Serviva un approccio più ragionato per risolvere il problema. - A quei tempi ero un “newbie” dell’informatica e quindi non conoscevo particolari tecniche se non l’utilizzo di procedure ricorsive, che avevo già  ampiamente utilizzato nel mio primo programma. Dovevo cercare un metodo che mi permettesse di risolvere il macro-problema risolvendo delle sue versioni più piccole. Quello che oggi viene chiamato un approccio Divide-et-Impera. Come potevo risolvere una matrice 10x10 in pezzi più piccoli? Ovviamanete dividendola in 4 sotto-matrici 5x5. Mi era venuto un lampo di genio. Potevo cercare di completare le 4 sotto-matrici 5x5 e quindi riempire tutta la matrice originale 10x10. L’idea era partire dalla matrice A, completarla, saltare nella sotto-matrice B, completarla, saltare nella sotto-matrice C, completarla ed infine saltare nell’‘ultima sotto-matrice D e completarla (vedi Figura 3). Ed a questo punto avrei risolto il problema iniziale.

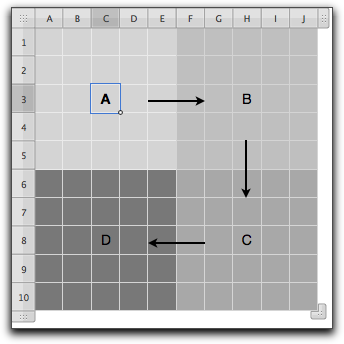
Figura 3 - Suddivisione del problema principale in 4 sotto-matrici 5x5

Ho modificato il mio programmino in C per fare un calcolo con matrici 5x5 et voilà applicato 4 volte mi ha completato le 4 sotto-matrici risolvendo il problema che aveva assillato i miei compagni, il tutto spendendo qualche giornata di programmazione e un po’ di sano brainstorming.

Riporto per completezza la soluzione (Figura 4) trovata a quel tempo.

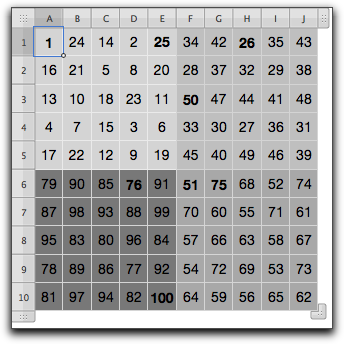
Figura 4 - Soluzione

Per chi si vuole cimentare sarebbe interessante trovare altre soluzioni, magari con altri metodi di risoluzione. Vedere quante sono esattamene le permutazioni possibili. Trovare il numero delle soluzioni possibili. Potrebbe essere interessante anche una formulazione più matematica del problema.

Pubblico di seguito la soluzione 12x12 condivisa gentilmente da Matteo Benedusi.

Figura 5 - Soluzione 12x12 di Matteo Benedusi